Định nghĩa hình tứ giác, Tính chu vi hình tứ giác lớp 2. Trong bài viết ngày hôm nay, svnckh sẽ gửi đến các bạn những nội dung chính chi tiết và đầy đủ nhất giúp các em cũng như phụ huynh về định nghĩa và cách giải bài tập chính xác nhất. Mời các bạn cùng xem dưới bài viết này nhé.
Định nghĩa hình tứ giác là gì?
Tứ giác là một đa giác có 4 cạnh và 4 đỉnh. Tổng các góc của tứ giác là 360 độ. Có nhiều loại tứ giác khác nhau. Có thể là tứ giác hoặc tứ giác kép. Trong tứ giác đơn lại có lồi hoặc lõm.
Tính chất của hình tứ giác
Trong hình tứ giác gồm có 2 tính chất đó là:
Tính chất 1:Tính chất hình chéo
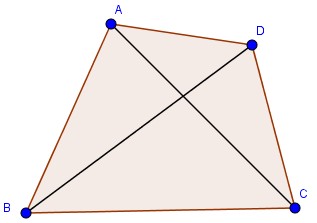
Trong một tứ giác lồi, hai đường chéo cắt nhau tại một điểm thuộc miền trong của tứ giác.
Ngược lại, nếu một tứ giác có hai đường chéo cắt nhau tại một điểm thuộc miền trong của nó thì tứ giác ấy là tứ giác lồi.
Tính chất 2: Tính chất góc của hình tứ giác
Tổng các góc của tứ giác bằng 360 độ.
Tìm hiểu thêm : Cách tính diện tích hình tứ giác
Các dạng tứ giác thường gặp
Tứ giác lõm là gì?
Định nghĩa tứ giác lõm? Tứ giác lõm là tứ giác chứa một góc trong có số đo lớn hơn 180° và một trong hai đường chéo nằm bên ngoài tứ giác.
Tứ giác không đều là gì?
Định nghĩa tứ giác không đều?
Là tứ giác mà nó không có cặp cạnh nào song song với nhau. Tứ giác không đều thường được dùng để đại diện cho tứ giác lồi nói chung (không phải là tứ giác đặc biệt).
Tứ giác đơn là gì?
Định nghĩa tứ giác đơn? Tứ giác đơn là bất kỳ tứ giác nào không có cạnh nào cắt nhau.
Tứ giác lồi là gì?
Định nghĩa tứ giác lồi?
Tứ giác lồi là tứ giác mà tất cả các góc trong nó đều nhỏ hơn 180° và hai đường chéo đều nằm bên trong tứ giác. Hay dễ hiểu hơn thì tứ giác lồi là tứ giác luôn nằm gọn trong một nửa mặt phẳng có chứa bất kỳ cạnh nào.
Các hình tứ giác đặc biệt
Hình chữ nhật
Định nghĩa hình chữ nhật là gì?
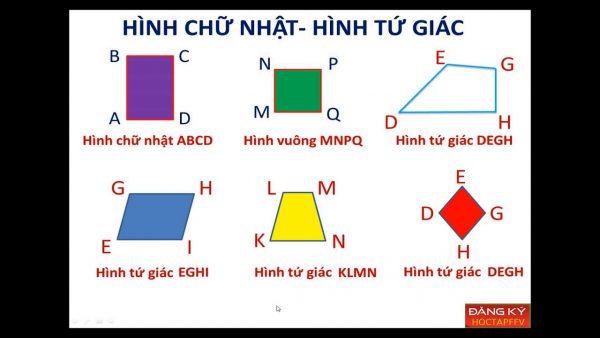
Hình chữ nhật: Hình chữ nhật là hình tứ giác có 4 góc vuông. Một điều kiện tương đương là 2 đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Hình vuông: có 4 góc vuông và 4 cạnh bằng nhau. Hình vuông có các cạnh đối song song (hình vuông là một hình bình hành), các đường chéo bằng nhau và vuông góc tại trung điểm. Một tứ giác là một hình vuông nếu và chỉ nếu nó vừa là một hình thoi vừa là một hình chữ nhật (bốn cạnh bằng nhau và bốn góc bằng nhau).
Tứ giác nội tiếp
Định nghĩa tứ giác nội tiếp là gì?
Trong hình học phẳng, một tứ giác nội tiếp là một tứ giác mà cả 4 đỉnh đều nằm trên một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp, và các đỉnh của tứ giác được gọi là đồng viên. Tâm đường tròn và bán kính lần lượt được gọi là tâm đường tròn ngoại tiếp và bán kính ngoại tiếp. Thông thường tứ giác nội tiếp là tứ giác lồi, nhưng cũng tồn tại các tứ giác nội tiếp lõm. Các công thức trong bài viết sẽ chỉ áp dụng cho tứ giác lồi.
Mọi tam giác đều có một đường tròn nội tiếp, nhưng không phải tất cả tứ giác đều nội tiếp. Một ví dụ cho một tứ giác không nội tiếp là một hình bình hành không là hình chữ nhật.
Tìm hiểu thêm : Cách vẽ biểu đồ đường gấp khúc trong excel
Hình thang
Định nghĩa hình thàng là gì?
Hình thang: là hình tứ giác có ít nhất 2 cạnh đối song song.
định nghĩa hình tứ giác và hình thang Định nghĩa hình tứ giác, các hình tứ giác phổ biến và đặc điểm
Hình thang cân: là hình thang có 2 góc kề cùng một cạnh đáy bằng nhau. Hoặc là hình thang với 2 đường chéo bằng nhau.
định nghĩa hình tứ giác và hình thang cân Định nghĩa hình tứ giác, các hình tứ giác phổ biến và đặc điểm
Hình bình hành
Định nghĩa hình bình hành là gì?
Hình bình hành: Hình bình hành là hình tứ giác có 2 cặp cạnh đối song song. Trong hình bình hành thì các cạnh đối bằng nhau, các góc đối bằng nhau, đường chéo cắt nhau tại trung điểm mỗi đường. Hình bình hành là trường hợp đặc biệt của hình thang.
định nghĩa hình tứ giác và hình bình hành Định nghĩa hình tứ giác, các hình tứ giác phổ biến và đặc điểm
Hình thoi: Hình thoi là hình tứ giác có 4 cạnh bằng nhau.
Hình thoi có 2 đường chéo vuông góc tại trung điểm mỗi đường và đường chéo là đường phân giác các góc. Hình thoi là một trường hợp đặc biệt của hình bình hành.
Ví dụ
Bài 1: Tính tổng các góc ngoài của tứ giác trong hình vẽ dưới đây:
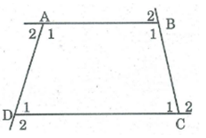
Hướng dẫn giải :
Ta có: ∠A1 + ∠B1 + ∠C1 + ∠D1 = 360 ̊ ( tính chất góc của hình tứ giác)
Mặt khác : ∠A1 + ∠A2 = 180 ̊ ( hai góc kề bù).
∠B1+ ∠B2= 180 ̊ (hai góc kề bù)
∠C1+ ∠C2= 180 ̊ (hai góc kề bù)
∠D1+ ∠D2= 180 ̊ (hai góc kề bù)
→ ∠A1 + ∠A2 + ∠B1 + ∠B2 + ∠C1 + ∠C2 + ∠D1 + ∠D2 = 180 ̊.4 = 720 ̊
→ ∠A2 + ∠B2 + ∠C2 + ∠D2 = 720 ̊ – (∠A1 + ∠B1 + ∠C1 + ∠D1) = 720 ̊ – 360 ̊ = 360 ̊
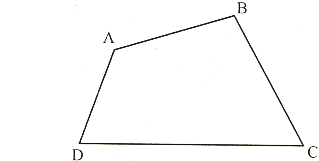
Bài 2: Trong các hình tứ giác sau đây, tứ giác nào là tứ giác luôn nằm trong nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tam giác?
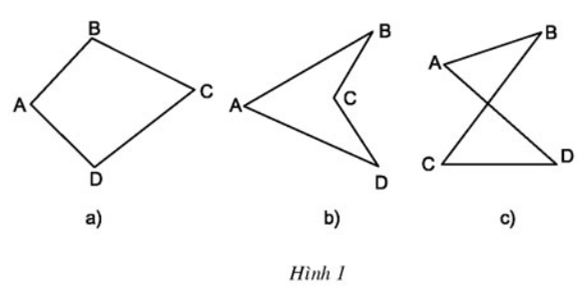
Lời giải:
Hình1a đúng: Vì là hình tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.
Hình 1b sai: Vì đó là tứ giác nằm trên hai nửa mặt phẳng có bờ BC (hoặc bờ CD).
Hình 1c sai: Vì tứ giác nằm trên hai nửa mặt phẳng có bờ AD (hoặc bờ BC).
Với nội dung bài viết chúng tôi đã tổng hợp lại lý thuyết cũng như bài tập liên quan về Định nghĩa hình tứ giác, Tính chu vi hình tứ giác lớp 2 sẽ giúp các em học tập tốt bộ môn toán học trong chương trình tiểu học. Xin cảm ơn.